publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
2024
-
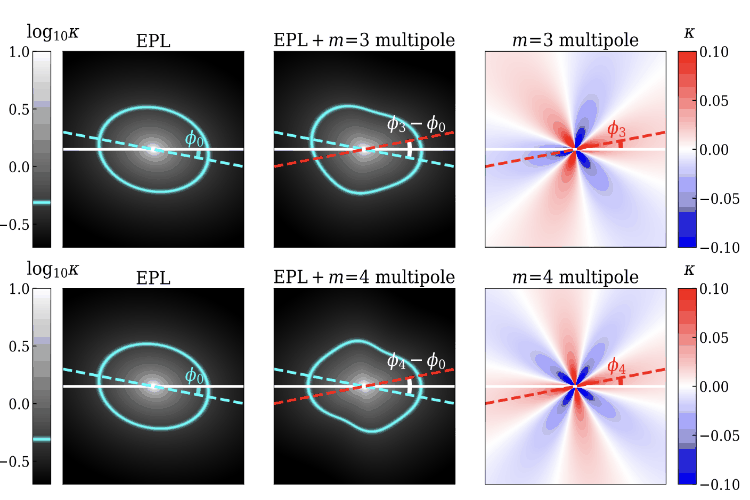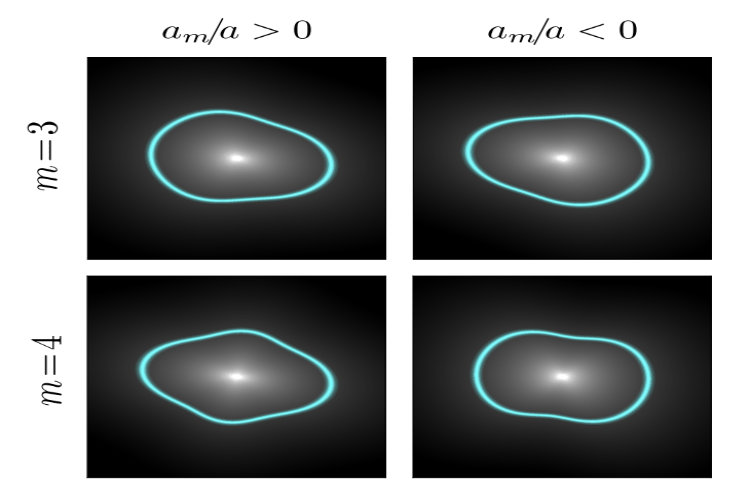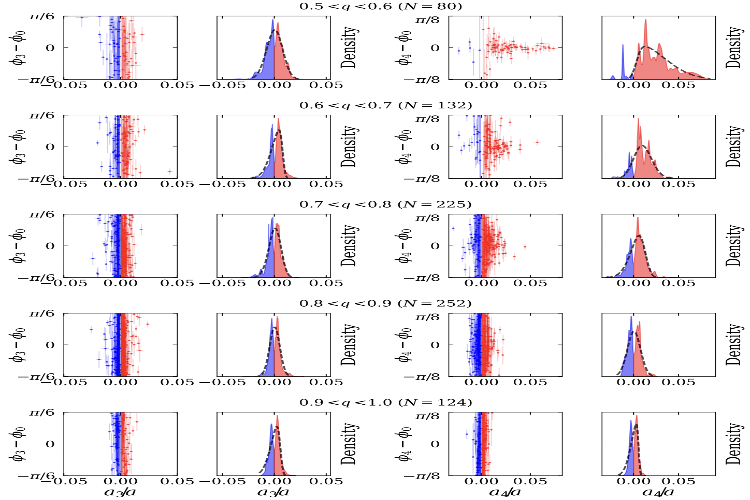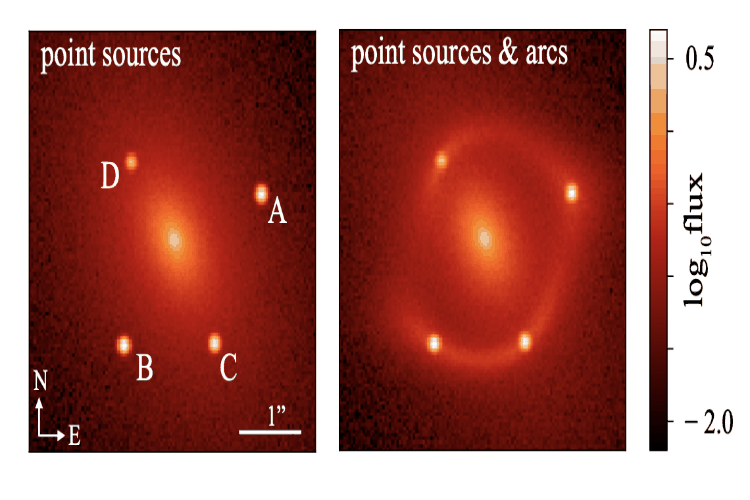Joint Semi-Analytic Multipole Priors from Galaxy Isophotes and Constraints from Lensed ArcsMaverick S. H. Oh, Anna Nierenberg, Daniel Gilman, and Simon Birrer2024Flux-ratio anomalies in quadruply imaged quasars are sensitive to the imprint of low-mass dark-matter haloes. The reliability of detection depends on the robustness of the smooth mass model. Optical surveys show that massive early-type galaxies similar to galaxy-scale gravitational lenses depart from perfect ellipticity, exhibiting m=3 and m=4 multipole distortions. We construct the semi-analytic, five-dimensional joint population prior for the m=3 and m=4 amplitude and orientation as well as the axis ratio of the deflector, calibrated on the sample of 840 SDSS E/S0 galaxies. The parameters are fitted via hierarchical Bayesian modeling, minimizing a joint Jensen-Shannon divergence between model and data. We use this prior to model the mass distribution of mock lenses with HST quality data with different multipole amplitudes. We find that we robustly measure the true multipole amplitudes and orientations. Compared to fits that use only the four point-image positions, adding the lensed host-galaxy arcs tightens the 68 % credible regions of multipole parameters by factors of 3-12 and reduces the predicted flux-ratio uncertainties by a mean factor of 6. This analysis does not include substructure or a complex source, and thus can be considered an upper limit on the expected improvement. The combination of arc information and realistic multipole priors therefore yields an order-of-magnitude improvement in smooth mass model precision, paving the way for more robust measurements of dark-matter substructure.
@misc{oh2024improving, title = {Joint Semi-Analytic Multipole Priors from Galaxy Isophotes and Constraints from Lensed Arcs }, author = {Oh, Maverick S. H. and Nierenberg, Anna and Gilman, Daniel and Birrer, Simon}, year = {2024}, eprint = {2404.17124}, archiveprefix = {arXiv}, primaryclass = {astro-ph.CO} } -
Turbocharging constraints on dark matter substructure through a synthesis of strong lensing flux ratios and extended lensed arcsDaniel Gilman, Simon Birrer, Anna Nierenberg, and Maverick S. H. Oh2024Strong gravitational lensing provides a purely gravitational means to infer properties of dark matter halos and thereby constrain the particle nature of dark matter. Strong lenses sometimes appear as four lensed images of a background quasar accompanied by spatially-resolved emission from the quasar host galaxy encircling the main deflector (lensed arcs). We present methodology to simultaneously reconstruct lensed arcs and relative image magnifications (flux ratios) in the presence of full populations of subhalos and line-of-sight halos. To this end, we develop a new approach for multi-plane ray tracing that accelerates lens mass and source light reconstruction by factors of ∼100−1000. Using simulated data, we show that simultaneous reconstruction of lensed arcs and flux ratios isolates small-scale perturbations to flux ratios by dark matter substructure from uncertainties associated with the main deflector mass profile on larger angular scales. Relative to analyses that use only image positions and flux ratios to constrain the lens model, incorporating arcs strengthens likelihood ratios penalizing warm dark matter (WDM) with a suppression scale mhm/M⊙ in the range [10^7−10^7.5], [10^7.5−10^8], [10^8−10^8.5], [10^8.5−10^9] by factors of 1.3, 2.5, 5.6, and 13.1, respectively, for a cold dark matter (CDM) ground truth. The 95% exclusion limit improves by 0.5 dex in log_10 mhm. The enhanced sensitivity to low-mass halos enabled by these methods pushes the observational frontier of substructure lensing to the threshold of galaxy formation, enabling stringent tests of any theory that alters the properties of dark matter halos.
@misc{gilman2024turbocharging, title = {Turbocharging constraints on dark matter substructure through a synthesis of strong lensing flux ratios and extended lensed arcs}, author = {Gilman, Daniel and Birrer, Simon and Nierenberg, Anna and Oh, Maverick S. H.}, year = {2024}, eprint = {2403.03253}, archiveprefix = {arXiv}, primaryclass = {astro-ph.CO} } -
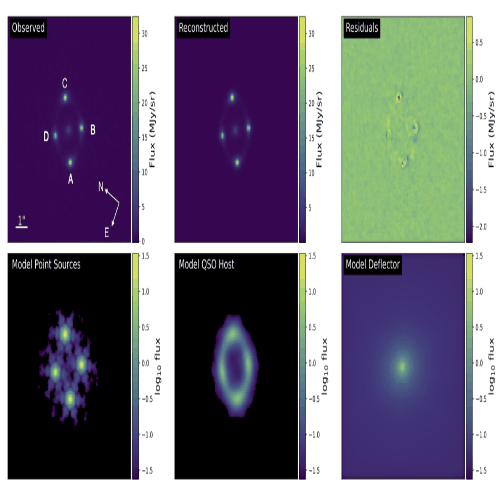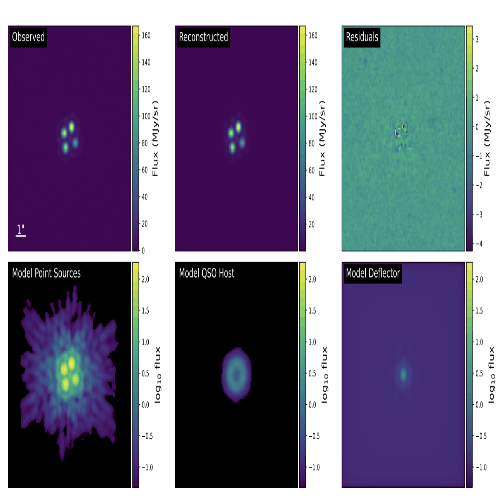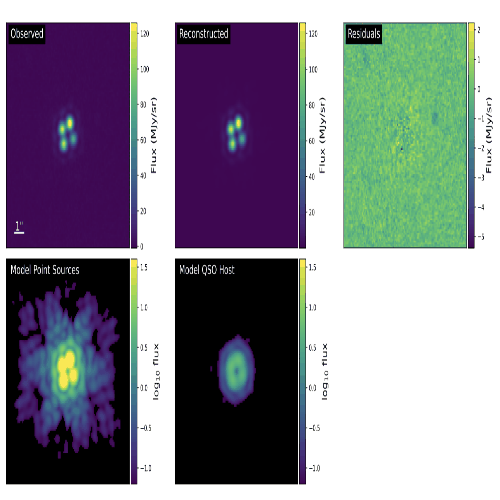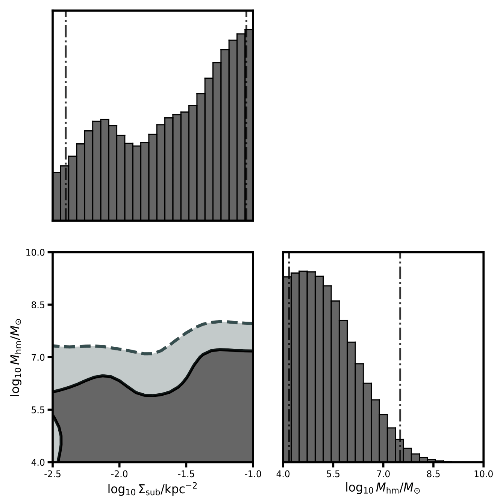JWST Lensed quasar dark matter survey II: Strongest gravitational lensing limit on the dark matter free streaming length to dateRyan E. Keeley, Anna M. Nierenberg, Daniel Gilman, Charles Gannon, Simon Birrer, Tommaso Treu, Andrew J. Benson, Xiaolong Du, K. N. Abazajian, T. Anguita, and 13 more authors2024@misc{keeley2024jwst, title = {JWST Lensed quasar dark matter survey II: Strongest gravitational lensing limit on the dark matter free streaming length to date}, author = {Keeley, Ryan E. and Nierenberg, Anna M. and Gilman, Daniel and Gannon, Charles and Birrer, Simon and Treu, Tommaso and Benson, Andrew J. and Du, Xiaolong and Abazajian, K. N. and Anguita, T. and Bennert, V. N. and Djorgovski, S. G. and Gupta, K. K. and Hoenig, S. F. and Kusenko, A. and Lemon, C. and Malkan, M. and Motta, V. and Moustakas, L. A. and Oh, M. S. H. and Sluse, D. and Stern, D. and Wechsler, R. H.}, year = {2024}, eprint = {2405.01620}, archiveprefix = {arXiv}, primaryclass = {astro-ph.CO} }
2023
2022
-
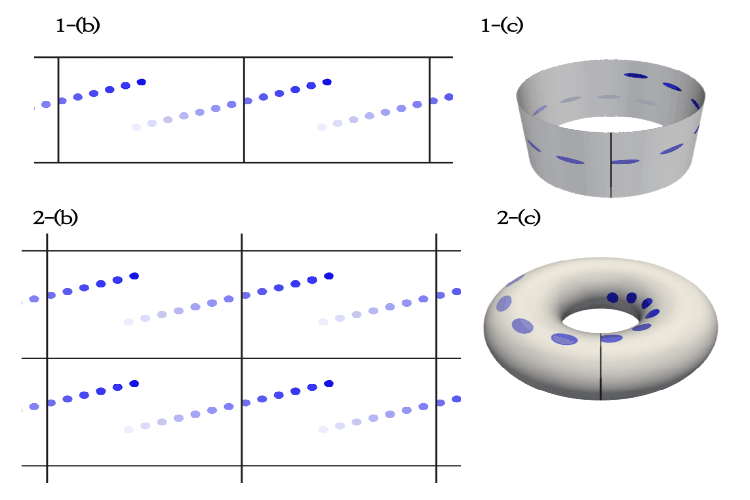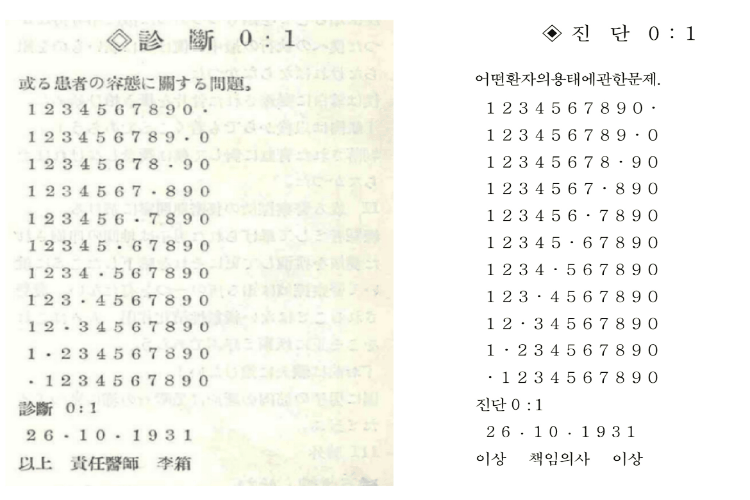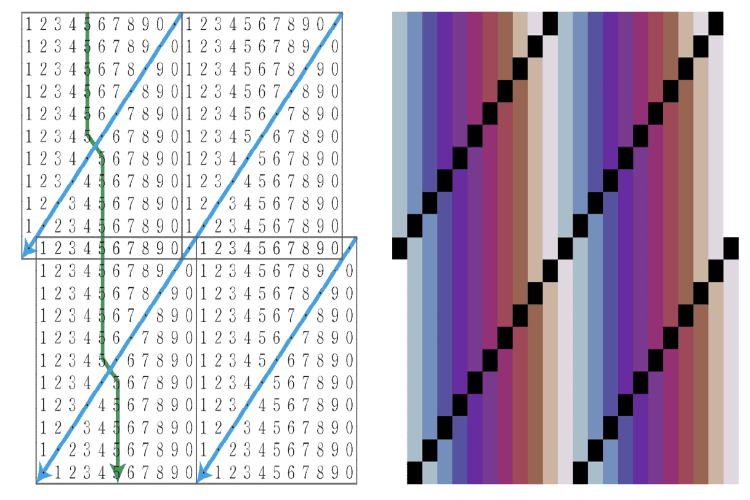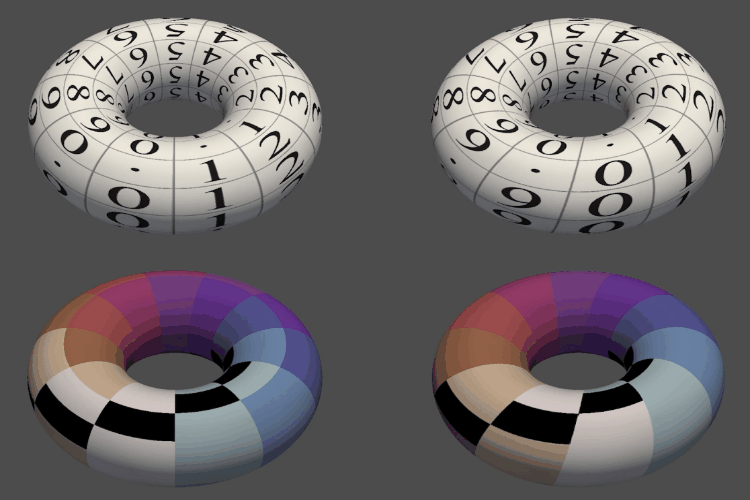이상 시의 주기경계조건 1– 「건축무한육면각체 - 진단 0:1」의 파해 Design and Periodic Boundary Condition of Yi-Sang’s Poems 1 –「Building Infinite-Hexahedral-Angle Bodies - Diagnosis 0:1」 DecryptionMaverick S. H. Oh, and Soo Jong LeeYiSang Review 2022이 논문 시리즈는 이상(李箱, 본명 김해경(金海卿), 1910-1937)의 작품 속에 나타난 주기경계조건(periodic boundary condition, PBC) 모티프를 규명·활용하여 난해시의 해석과 이상 문학의 더 깊은 이해를 도모한다. 이 논문은 시리즈를 여는 첫 번째 논문으로서, 그간 명확한 해석이 부재했던 난해시 「건축무한육면각체 - 진단 0:1」(1932)의 해석을 통해 주기경계조건 모티프를 실증한다. 주기경계조건이란 (시)공간의 경계가 연결되어 무한한 주기성을 가짐을 의미한다. 이는 4차원 시공간에 더해 주기경계조건을 갖춘 공간을 문학의 대상이자 배경으로 삼은 것으로, 1936년의 차원주의자 선언으로 정립된 예술운동인 차원주의보다 전위적으로 선취된 문학적 시도로 볼 수 있다. 주기경계조건 모티프는 기존에 연구되었던 다양한 모티프와 긴밀한 관계를 갖는다. 논문 소개 동영상: https://www.youtube.com/watch?v=VT7J85OtCFc. This paper series investigates and utilizes the periodic boundary condition (PBC) motif that appeared in the works of Yi-Sang (real name Kim Hae-Gyeong, 1910-1937) to interpret his difficult poems and understand his literature more deeply. This paper, as the first work of the series, proves the PBC motif by successfully interpreting the difficult poem “Building Infinite Hexahedral-Angle Bodies - Diagnosis 0:1”, which has not been clearly explained thus far. The periodic boundary condition means that the boundary of space (or spacetime) is connected and has infinite periodicity. It is earlier and potentially more advanced than Dimensionism, which was established by Dimensionist Manifesto in 1936, in the sense that it takes spacetime not only of 4-dimension but also with periodic boundary condition as an object and a background of literature. Periodic boundary condition motif has a close relationship with various previously studied motifs. Summary video: https://www.youtube.com/watch?v=VT7J85OtCFc
@article{Maverick2022Yi-Sang, title = {이상 시의 주기경계조건 1– 「건축무한육면각체 - 진단 0:1」의 파해 Design and Periodic Boundary Condition of Yi-Sang’s Poems 1 –「Building Infinite-Hexahedral-Angle Bodies - Diagnosis 0:1」 Decryption}, author = {Oh, Maverick S. H. and Lee, Soo Jong}, journal = {YiSang Review}, volume = {18}, pages = {1--32}, year = {2022}, publisher = {The Society of YiSang}, note = {Written in Korean.} }
2021
-
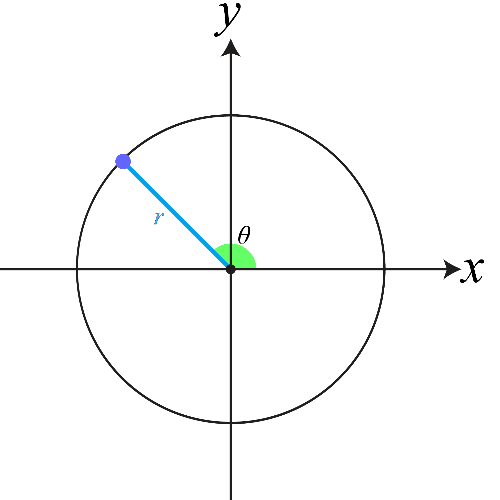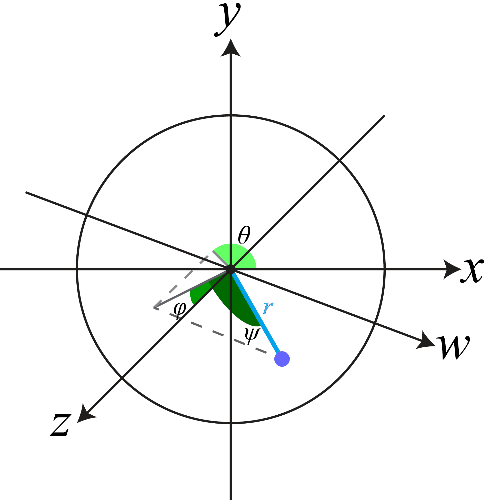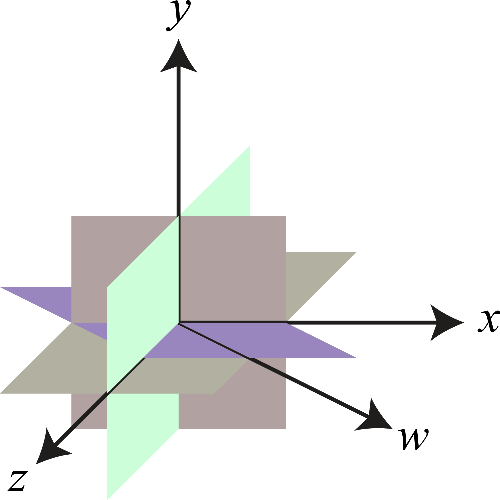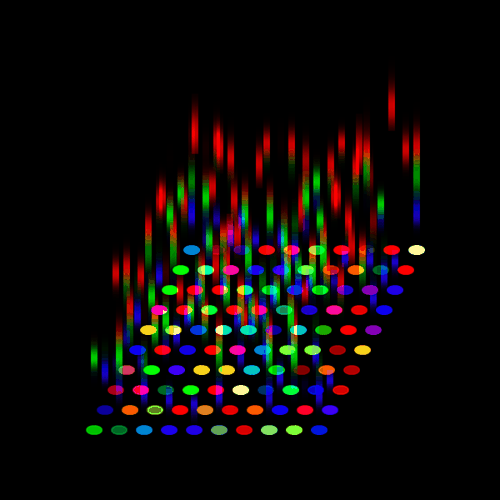이상 시의 4차원 시공간 설계 및 건축: 삼차각설계도와 건축무한육면각체의 연결, 그리고 차원 확장 Design and Construction in Four-Dimensional Space-Time in Yi-Sang’s Poems: The Connection Between Three-Dimensional Angle Blueprint and Building Infinite-Hexahedral-Angle Bodies, and Dimension ExpansionMaverick S. H. Oh, and Soo Jong LeeJournal of Korean Culture (JKC) 2021이 논문은 이상(李箱, 본명 김해경(金海卿), 1910-1937)의 연작시 「삼차각설계도(三次角設計圖)」와 「건축무한육면각체(建築無限六面角體)」에 나타난 기하학적․물리학적 원관념에 대한 보다 구체적이고 정합적인 이해의 기조를 세우기 위한 시도이다. 이상은 당대 최신의 물리학 이론에 대한 이해를 바탕으로 4차원상에서 임의의 도형을 설계․건축하는 시도를 연작시에 남겼고, 이 과정에서 ‘삼차각’과 ‘육면각체’라는 조어를 직접 만들어 사용하였다. 이 논문은 ‘삼차각’이란 4차원 공간상에서 물체의 물리적 위치를 초구면좌표계로 나타낼 때 필요한 세 개의 각도값임을, 그리고 ‘육면각’이란 삼차각의 적분으로 얻어지는 초입체각이며, 그와 동시에 4차원상에서 한 점에서 만나는 여섯 개의 면이 이루는 각임을 해설한다. 또한 n개의 점과 그에 대응하는 육면각으로 이루어진 도형을 n-육면각체라고 부를 수 있고, 그에 따라 ‘무한-육면각체’가 4차원상의 임의의 도형을 의미함을 해설한다. 아울러, 「선에관한각서1」과 「AU MAGASIN DE NOUVEAUTES」에 나타난 차원 확장에 대해 다룬다.논문 소개 동영상: https://youtu.be/hoH1GrumJ58. This paper is a trial to establish the foundation of more concrete and coherent understanding of two series poems of Yi-Sang, 「Three-Dimensional Angle Blueprint(삼차각설계도, 三次角設計圖,)」 and 「Building Infinite Hexahedral-Angle Bodies(건축무한육면각체, 建築無限六面角體)」. Yi-Sang, based on his understanding on contemporary physics theories, wrote about his attempt to design and build arbitrary four-dimensional bodies on the poems. He coined and used the terms ‘three-dimensional angle’ and ‘hexahedral-angle body’. In this paper, it is explained that a three-dimensional angle is the set of three angular values from expressing the physical position of an object in four-dimensional space using the hyperspherical coordinate system, and a ‘hexahedral angle’ is the hyper-solid angle calculated from the integration of a three-dimensional angle as well as the angle made with six intersecting planes. Also, it is shown that a body that has n vertices and corresponding hexahedral angles can be called as n-hexahedral-angle body, which is followed by the notion that an ‘infinite-hexahedral-angle body’ is an arbitrary body in the four-dimensional space. On top of that, the dimension expansion that appears in 「Memorendum on lines 1」 and 「AU MAGASIN DE NOUVEAUTES」 is covered. Summary video: https://youtu.be/hoH1GrumJ58
@article{Maverick2021Yi-Sang, title = {이상 시의 4차원 시공간 설계 및 건축: 삼차각설계도와 건축무한육면각체의 연결, 그리고 차원 확장 Design and Construction in Four-Dimensional Space-Time in Yi-Sang’s Poems: The Connection Between Three-Dimensional Angle Blueprint and Building Infinite-Hexahedral-Angle Bodies, and Dimension Expansion}, author = {Oh, Maverick S. H. and Lee, Soo Jong}, journal = {Journal of Korean Culture (JKC)}, volume = {54}, pages = {107--156}, year = {2021}, publisher = {The International Academic Forum of Korean Language and Literature}, note = {Written in Korean.} } -
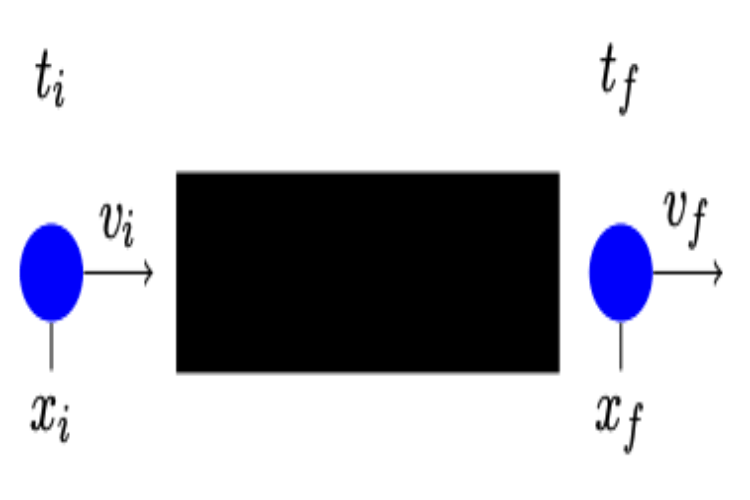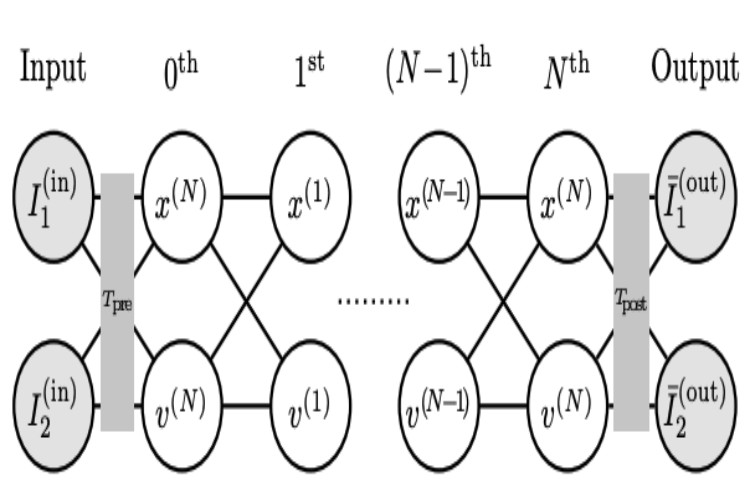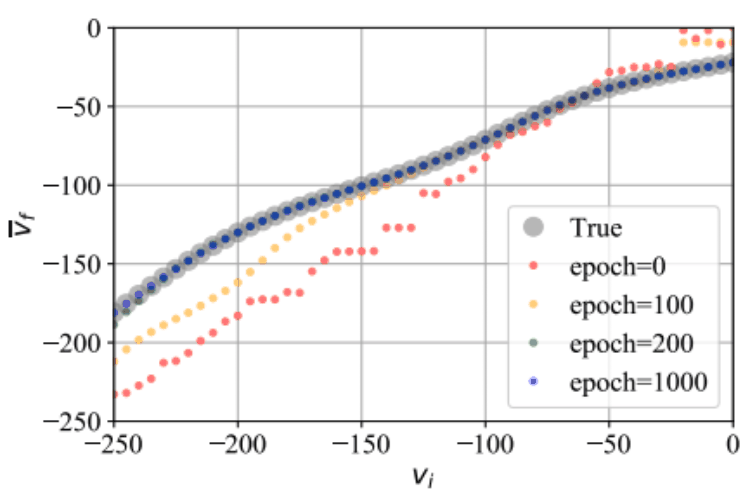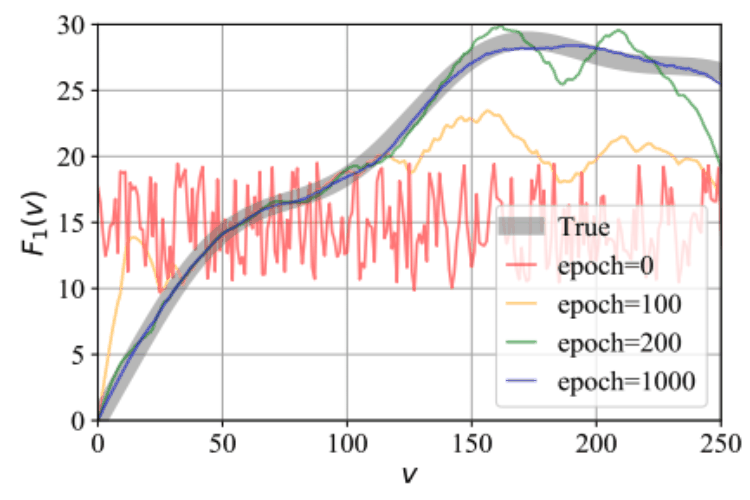AdS/Deep-Learning made easy: simple examplesMugeon Song, Maverick S. H. Oh, Yongjun Ahn, and Keun-Young KimChinese Physics C Jul 2021Deep learning has been widely and actively used in various research areas. Recently, in gauge/gravity duality, a new deep learning technique called AdS/DL (Deep Learning) has been proposed. The goal of this paper is to explain the essence of AdS/DL in the simplest possible setups, without resorting to knowledge of gauge/gravity duality. This perspective will be useful for various physics problems: from the emergent spacetime as a neural network to classical mechanics problems. For prototypical examples, we choose simple classical mechanics problems. This method is slightly different from standard deep learning techniques in the sense that we not only have the right final answers but also obtain physical understanding of learning parameters.
@article{song2021ads, doi = {10.1088/1674-1137/abfc36}, year = {2021}, month = jul, publisher = {{IOP} Publishing}, volume = {45}, number = {7}, pages = {073111}, author = {Song, Mugeon and Oh, Maverick S. H. and Ahn, Yongjun and Kim, Keun-Young}, title = {AdS/Deep-Learning made easy: simple examples}, journal = {Chinese Physics C} } -
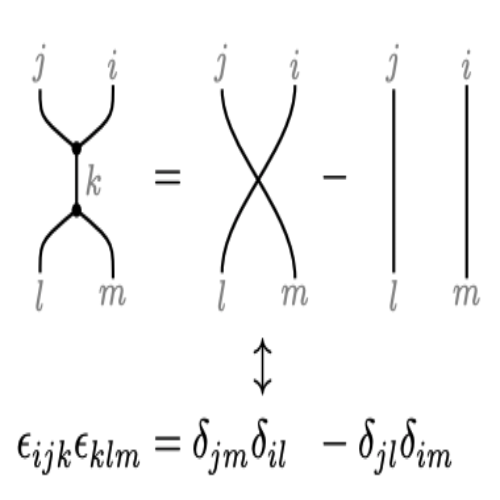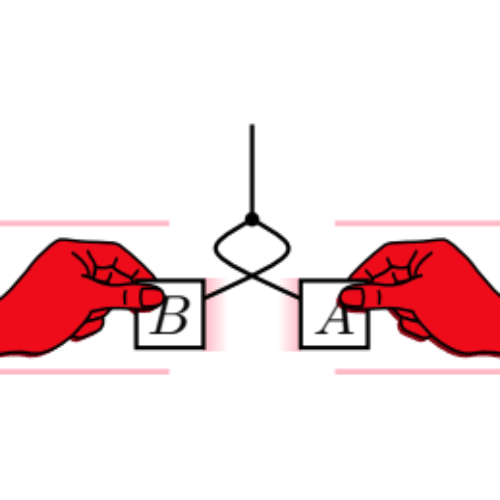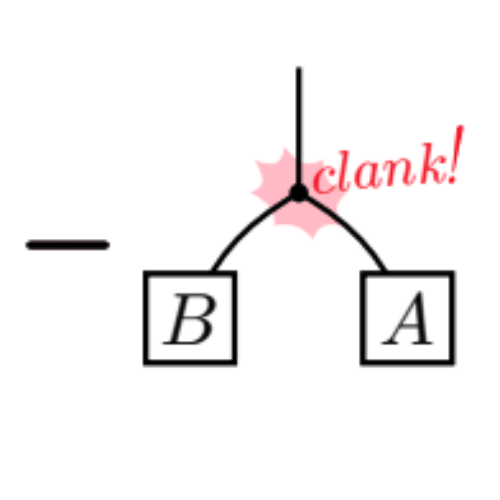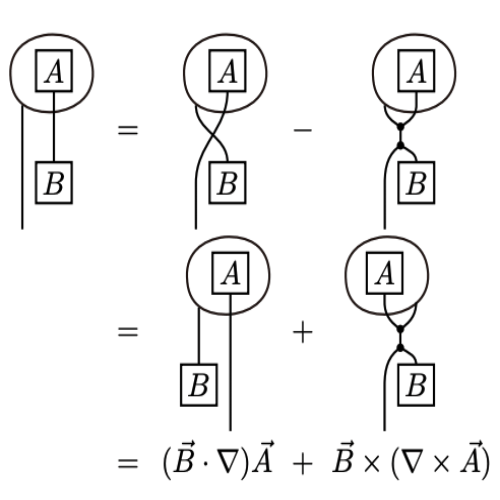Boosting vector calculus with the graphical notationJoon-Hwi Kim, Maverick S. H. Oh, and Keun-Young KimAmerican journal of physics Jul 2021Learning vector calculus techniques is one of the major hurdles faced by physics undergraduates. However, beginners report various difficulties dealing with the index notation due to its bulkiness. Meanwhile, there have been graphical notations for tensor algebra that are intuitive and effective in calculations and can serve as a quick mnemonic for algebraic identities. Although they have been introduced and applied in vector algebra in the educational context, to the best of our knowledge, there have been no publications that employ the graphical notation to three-dimensional Euclidean vector calculus, involving differentiation and integration of vector fields. Aiming for physics students and educators, we introduce such “graphical vector calculus,” demonstrate its pedagogical advantages, and provide a variety of exercises containing both purely mathematical identities and practical calculations in physics. The graphical notation can readily be utilized in the educational environment to not only lower the barriers in learning and practicing vector calculus but also make students interested and self-motivated to manipulate the vector calculus syntax and, on their own, heuristically comprehend the language of tensors.
@article{kim2021boosting, title = {Boosting vector calculus with the graphical notation}, author = {Kim, Joon-Hwi and Oh, Maverick S. H. and Kim, Keun-Young}, journal = {American journal of physics}, volume = {89}, number = {2}, pages = {200--209}, year = {2021}, publisher = {American Association of Physics Teachers}, doi = {10.1119/10.0002142} } -
An Invitation to Graphical Tensor Methods : Exercises in Graphical Vector and Tensor Calculus and MoreJoon-Hwi Kim, Maverick S. H. Oh, and Keun-Young KimJul 2021This is the supplementary material for “Boosting Vector Calculus with the Graphical Notation.” It is written for students and introduces instructive and practical examples regarding graphical vector and tensor algebra and calculus in the physics context. Notable topics, including the ones mentioned in the main article, are as follows. Graphical proof of the Jacobi identity is discussed in P6a and its sequels in the following two sections. Next, most importantly, graphical proof of first and second derivative vector calculus identities are covered in Sections I B 1 and I B 2. Then, the strength of the graphical technique of tensor calculus is elaborated throughout Section I C. Graphical notation for general multi-index quantities is introduced in Section I C 2. Do not miss the next section, Section I C 3, to learn the “arrow pushing” that enables to efficiently denote and explain the invariance property of tensorial expressions. Finding the oblivious δ (3)( r) term and the calculus of multipolar fields are discussed throughout Sections I C 5 and I C 6. Section I A 4 introduces permutation symmetry of indices. Refer to the comments in A67b for an instructive example of diagrammatic perturbation in statistical mechanics. Lastly, Section I D invites the reader into the world of Feynman diagrams.
@misc{kim2019boosting2, title = {An Invitation to Graphical Tensor Methods : Exercises in Graphical Vector and Tensor Calculus and More}, author = {Kim, Joon-Hwi and Oh, Maverick S. H. and Kim, Keun-Young}, year = {2021}, note = {Supplementary material. }
2020
-
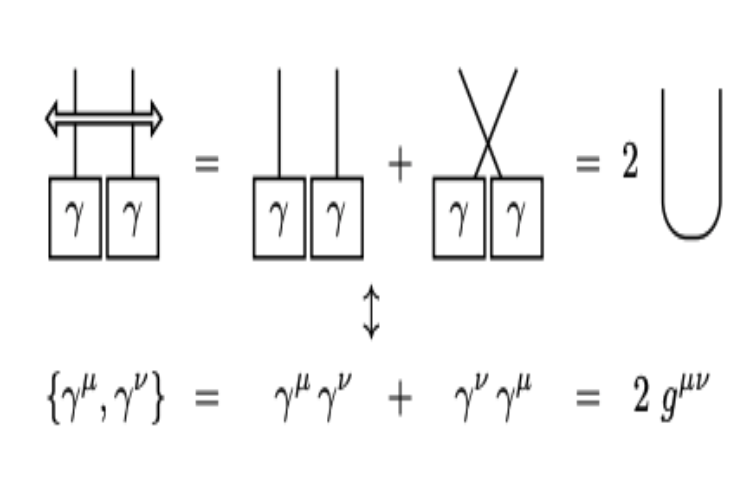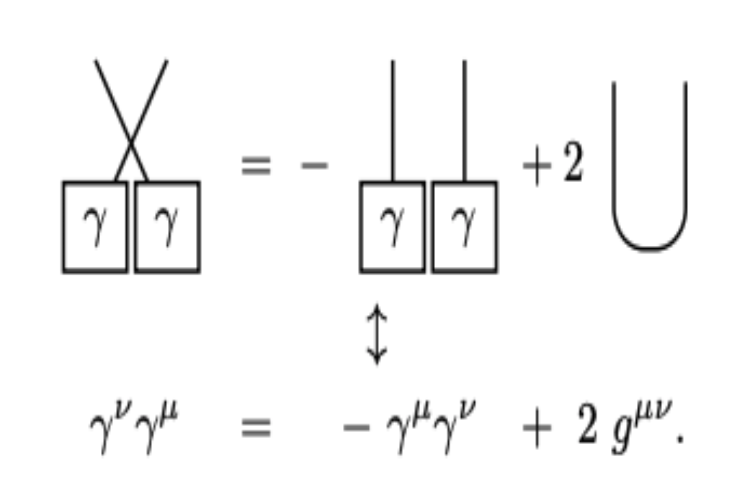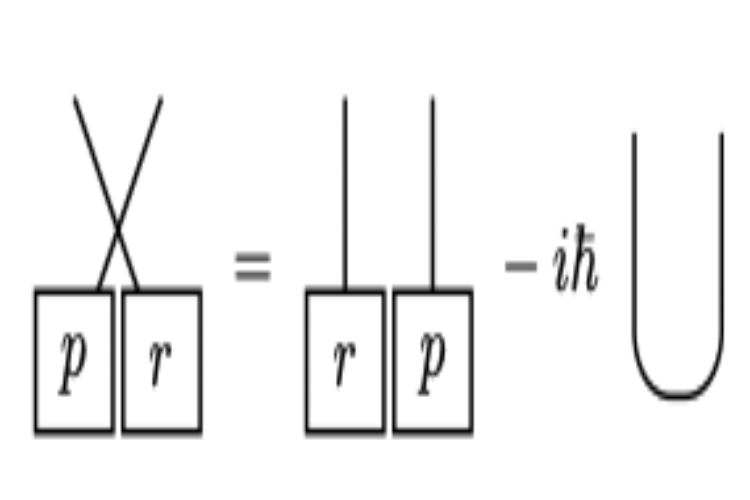Graphical Notation for Vector Calculus and Its GeneralizationMaverick S. H. OhJul 2020Graphical notation has been introduced and utilized in physics for years, but it still remains as relatively minor notation compared to the conventional plaintext notation despite its effectiveness, readability, and applicability. In this thesis, the graphical notation for vector calculus is reviewed and generalized. The essence and advantage of the graphical notation are illustrated with vector calculus as a self-contained example. Basic rules are introduced and utilized to prove some representative vector calculus identities, illustrating how concise and effective the graphical notation is. More generalized concepts and notations, such as the algebra of gamma matrices and quantum mechanical commutation relation, are reviewed to show how the notation can be modified and extended. By enabling graphical notation to be readily applied and taught in undergraduate level vector calculus, the entry barrier of graphical notation would be lowered and the practical use of the notation would be promoted. The generalization examples would encourage readers to manipulate and invent graphical notations by themselves when needed, enlarging and diversifying the use of graphical notation in general. This would lead to more concrete and efficient understanding and presentation of physics.
@misc{Maverick2020bsthesis, key = {bs}, author = {Oh, Maverick S. H.}, title = {Graphical Notation for Vector Calculus and Its Generalization}, howpublished = {Bachelor Thesis}, year = {2020}, }
2019
-
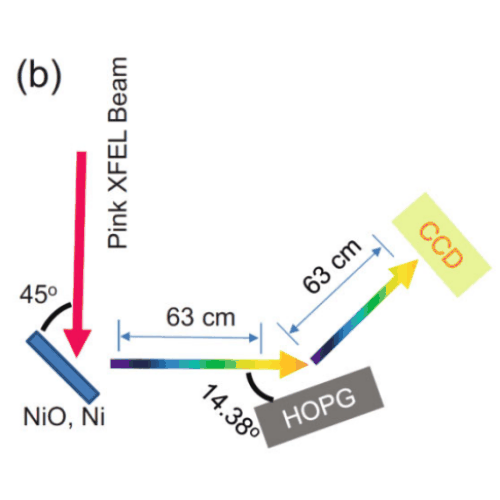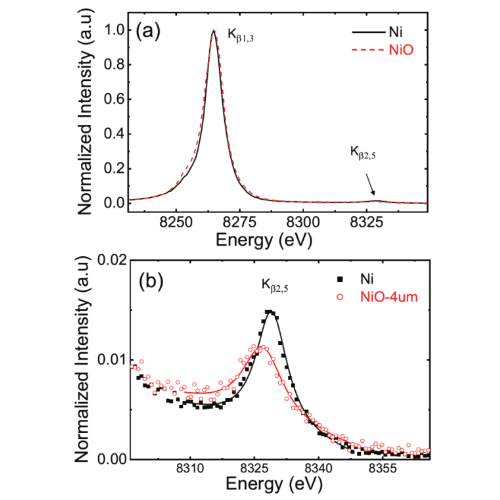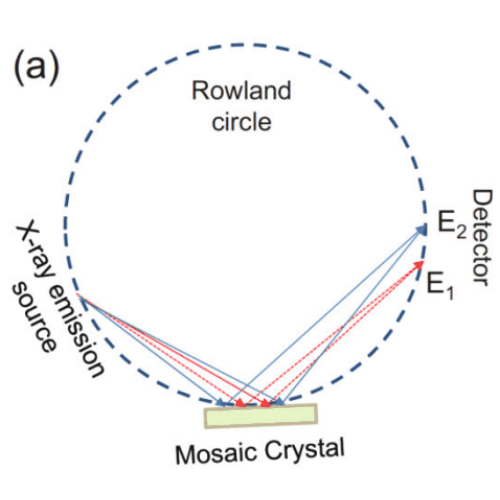Hard X-ray von Hamos Spectrometer for Single-Pulse Emission SpectroscopyMuhammad Ijaz Anwar, Sung Soo Ha, Byung-Jun Hwang, Seonghyun Han, Maverick S. H. Oh, Mohd Faiyaz, Do Young Noh, Hyon Chol Kang, and Sunam KimJournal of the Korean Physical Society Oct 2019We developed a hard X-ray spectrometer for the purpose of measuring X-ray emission spectrum excited by using single X-ray free electron laser (XFEL) pulses. A highly oriented pyrolytic graphite (HOPG) crystal was placed in the von Hamos geometry to focus X-rays of the equal energy on a specific point in detector plane. The spectrometer was tested at PAL-XFEL using Ni and NiO films. The Ni 𝐾𝛽13 X-ray emission line excited by using a single X-ray pulse was successfully resolved. If the much weaker Ni 𝐾𝛽25 line is to be observed, data must be accumulated with a few thousands of X-ray pulses. The spectrometer energy resolving power, E/ΔE, was estimated to be 7500. This spectrometer can be utilized to conduct various X-ray emission and absorption measurements using XFELs.
@article{Anwar2019, author = {Anwar, Muhammad Ijaz and Ha, Sung Soo and Hwang, Byung-Jun and Han, Seonghyun and Oh, Maverick S. H. and Faiyaz, Mohd and Noh, Do Young and Kang, Hyon Chol and Kim, Sunam}, title = {Hard X-ray von Hamos Spectrometer for Single-Pulse Emission Spectroscopy}, journal = {Journal of the Korean Physical Society}, year = {2019}, month = oct, day = {01}, volume = {75}, number = {7}, pages = {494--497}, note = {\href{https://doi.org/10.3938/jkps.75.494}{\url{doi.org/10.3938/jkps.75.494}}} }